Adjacency Lists

If you aren't familiar with graph theory, I advise you to read my post on minimum spanning trees, where I define several important graph-theoretic terms that are relevant to this entry.

There are a number of ways to represent a graph. For example, you can represent a graph as an adjacency matrix, as an edge list, or as an adjacency list. In my Python implementation of Kruskal's algorithm, I used an edge list.

Today I will discuss adjacency lists, because I'm going to use adjacency lists in some algorithms that I will post about soon.

The idea of an adjacency list is very simple. In its most basic form, an adjacency list is just a list that contains the adjacent vertices for a graph's vertices. For example, say that we have the following graph:

We can represent this graph by the adjacency list A = [[1, 2, 4], [0, 2], [0, 1, 5], [4], [0, 5, 6], [2, 4], [4]].

So, for vertex 0, we have A[0] = [1, 2, 4], which corresponds to the vertices that 0 is adjacent to in the graph. Likewise, for vertex 1, we have A[1] = [0, 2], which corresponds to the vertices that 1 is adjacent to. The same goes for all the other vertices. If we want to know which vertices are adjacent to a vertex v, then A[v] will give us the list of vertices adjacent to v.

More precisely, A[v] is the list of vertices that v has an out-edge to. We can use adjacency lists to represent both undirected graphs and directed graphs. In an undirected graph, we have edges between vertices. In a directed graph, we have edges from and to vertices. For example:

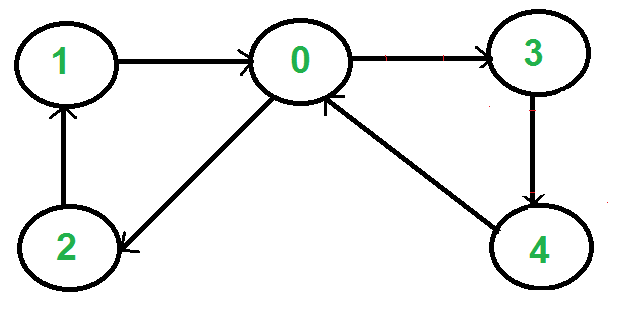
Here, the adjacency list is D = [[3], [0], [1], [4], [0]]. So, there is an edge from 0 to 3. However, there is no edge from 3 to 0. The edges have directions. Even if u is an element of D[v], v is not necessarily an element of D[u]. For example, 3 is an element of D[0], but 0 is not an element of D[3]. In contrast, in our first, undirected graph, if u was an element of A[v], then v was necessarily an element of A[u]. For example, because 1 is an element of A[0], 0 is an element of A[1]. We can say that, in this undirected graph, 1 and 0 both have out-edges to each other, while in the directed graph, 0 has an out-edge to 3, but 3 doesn't have an out-edge to 0.

You can represent a weighted graph with a list of lists of vertex-weight pairs. For example:

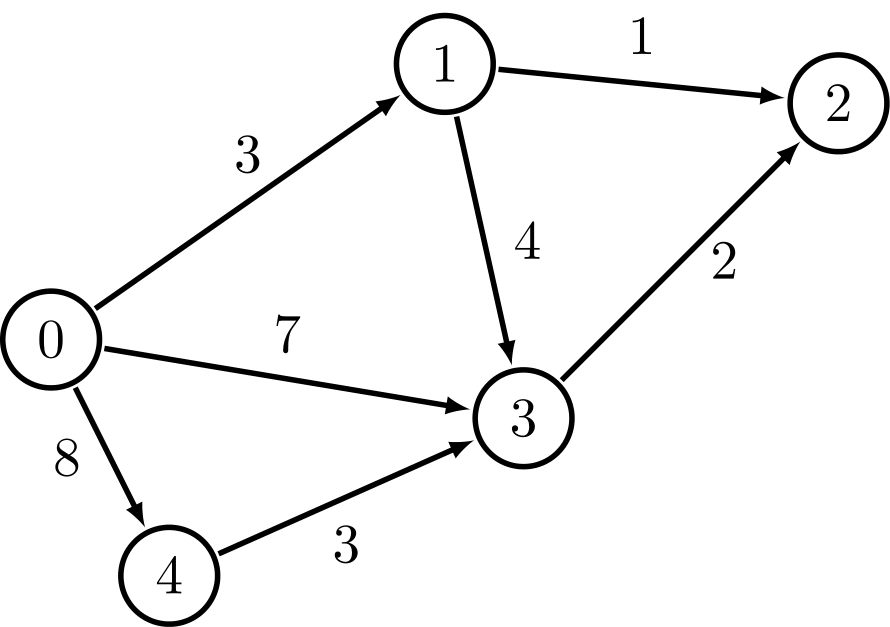
We can represent this graph as W = [[[1, 3], [3, 7], [4, 8]], [[2, 1], [3, 4]], [], [[2, 2]], [[3, 3]]].

So, W[0] = [[1, 3], [3, 7], [4, 8]], which represents the fact that vertex 0 has an edge to vertex 1 of weight 3, an edge to vertex 3 of weight 7, and an edge to vertex 4 of weight 8.

If the graph's vertices aren't numbered and you don't want to create a correspondence between the vertices and the nonnegative integers, then you can very easily implement an adjacency list with an associative array. The associative array's keys will be the vertices' names, and its values will be the names of adjacent vertices.