Minimum Spanning Trees

A minimum spanning tree of a weighted connected graph is a spanning tree whose weight is less than or equal to the weight of every other spanning tree of that graph.

But what does that mean? Because that statement might not be terribly clear, let's break it down:

Informally, a graph is a set of points called vertices that are joined by lines called edges. Formally, a graph is an ordered pair of sets (V, E), where V is a finite set of vertices and E is subset of V x V.

Here's an example of a graph:

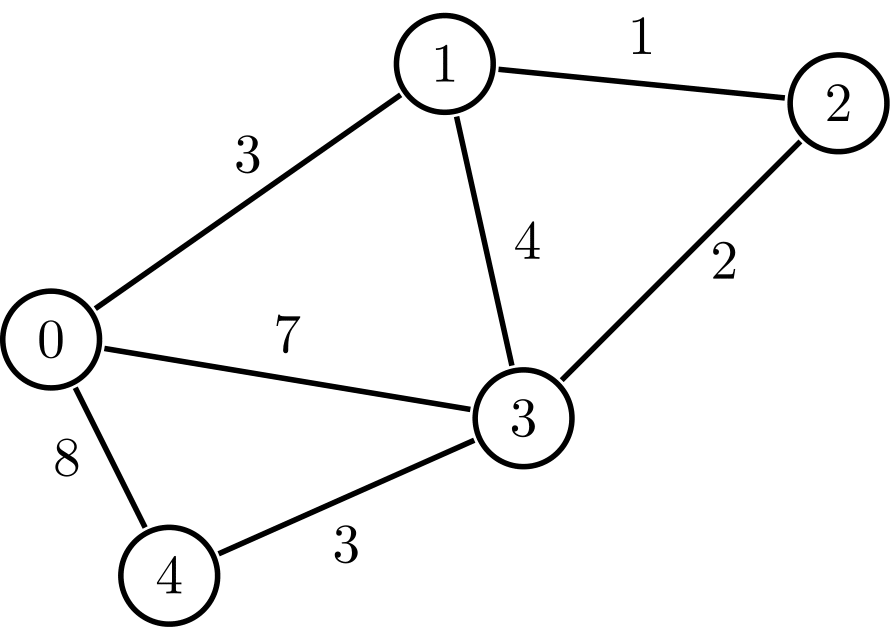
The lines are the edges, and the points are the vertices. The graph consists of the vertices and the edges.

You can see in the above image that the edges have numbers next to them. This graph is a weighted graph. A weighted graph has a number associated with each edge of the graph. Each number is a weight for that edge. The weight of a graph is the sum of all those numbers.

A walk consists of a finite sequence of vertices. Each pair of neighboring vertices has an edge between them. An example of a walk in the above graph is 0 -> 1 -> 3 -> 1 -> 2.

A trail is a walk that doesn't contain any repeat edges. An example of a trail in the above graph would be 0 -> 3 -> 1 -> 2 -> 3.

A path is a walk that doesn't contain any repeat vertices. An example of a path in the above graph is 0 -> 4 -> 3 -> 2 -> 1.

A cycle is a trail that begins and ends at the same vertex and doesn't contain any other repeat vertices. An example of a cycle in the above graph is 0 -> 1 -> 2 -> 3 -> 0.

An acyclic graph has no cycles. The above graph is cyclic. It contains several cycles.

A graph is connected if and only if, for every pair of vertices u and v, there is a path from u to v. The above graph is connected.

A tree is a connected, acyclic graph.

A tree spans a connected graph if and only if it contains all of the vertices of that graph. A spanning tree of a connected graph is a tree that spans the graph.

Now we can use these definitions to unpack our initial statement of what a minimum spanning tree is:

A minimum spanning tree is a tree. So, a minimum spanning tree is a graph that is (i) connected and (ii) acyclic. That means that (i) each pair of the graph's vertices has a path between them and that (ii) none of the graph's vertices has a path going back to itself.

As a spanning tree, a minimum spanning tree spans a connected graph. That means that it contains all of the vertices of that graph.

As a minimum spanning tree, a minimum spanning tree has a weight. Its weight is the sum of the weights of its edges. (To be clear, it derives its edges from the graph that it spans.)

What makes a minimum spanning tree be a minimum spanning tree is that its weight is less than or equal to the weight of every other spanning tree that spans that graph.

A minimum spanning tree for the above graph is:

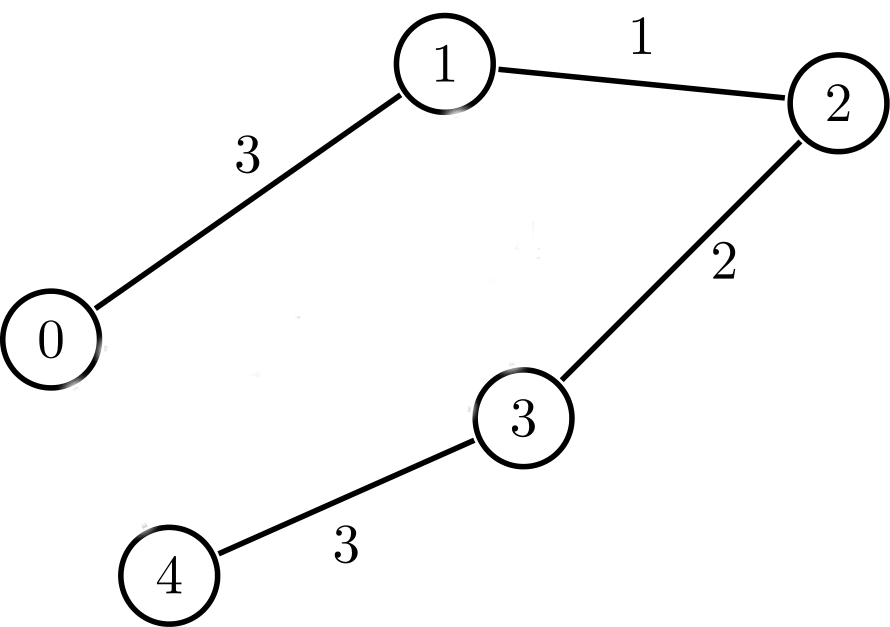
Hopefully, that clears up what a minimum spanning tree is. Now for the next question: Why are minimum spanning trees important?

Let's say there is a set of computers that you want to network together. Because it's expensive to network computers together, you want to find the least expensive way to connect all of them. In other words, you want to construct a minimum spanning tree! In general, minimum spanning trees let you connect a set of things that are costly to connect at the least possible expense. You can apply minimum spanning trees to road construction, social networks, circuit design, etc., etc.

Now your question should be: How do I find minimum spanning trees? The two most popular algorithms are Prim's algorithm and Kruskal's algorithm. I go over Kruskal's algorithm in this post.